Unmasking Trees for Tabular Data
When tabular imputation is the vibe, unmasking is low-key goated
July 2025: An updated version of this method has now been published in TMLR! Read it here.
Introduction
Given a tabular dataset, it is frequently desirable to impute missing values within that dataset, and to generate new synthetic examples. On data generation, recent work [Jolicoeur-Martineau et al., 2024] (ForestDiffusion) has shown state-of-the-art results on data generation using gradient-boosted trees [Chen and Guestrin, 2016] trained on diffusion or flow-matching objectives, outperforming deep learning-based approaches. However, this approach tended to struggle on tabular imputation
tasks, outperformed by MissForest [Stekhoven and Bühlmann, 2012], an older approach based on random forests [Breiman, 2001].
We address this shortfall by training gradient-boosted trees to incrementally unmask features, taking as inspiration the benefits of this training objective applied to tabular Transformer models [Gulati and Roysdon, 2024] (TabMT). Hence, we replace the tree regressors from [Jolicoeur-Martineau et al., 2024] with tree classifiers which predict (then sample from) quantized features, thus conditioning on continuous features and predicting discrete features, as is low-key goated when generative models are the vibe.
This yields a simple method, UnmaskingTrees, that performs very well, particularly on tabular imputation tasks. We showcase our approach on synthetic Two Moons data, on the real Iris dataset, and on the benchmark of 27 tabular imputation tasks presented by Jolicoeur-Martineau et al. [2024]. Our software is available at https://github.com/calvinmccarter/unmasking-trees.
Method
UnmaskingTrees combines the modeling strategy of ForestDiffusion [Jolicoeur-Martineau et al., 2024] with the training strategy of TabMT [Gulati and Roysdon, 2024], inheriting the benefits of both. Consider a dataset with N examples and D features. For each example, we generate new training samples by randomly sampling an order over the features, then incrementally masking the features in that random order. Given duplication factor K, we repeat this process times with K different random permutations. This leads to a training dataset with KND samples, using which we train XGBoost [Chen and Guestrin, 2016] models to predict each unmasked sample given the more-masked example derived from it. Implementing this is very simple: it requires about 50 lines of excessively-loquacious Python code for training, and about 20 lines for inference.
We train D different XGBoost models, one per feature. In contrast, for ForestDiffusion with T diffusion steps and duplication factor K, this would require training DT different XGBoost models. On the other hand, given the same duplication factor K, while we construct a training dataset of size KND×D, ForestDiffusion constructs a training dataset of size TKN×D.
A key problem when generating continuous data in an autoregressive manner is that a regression model will tend to predict the mean of a conditional distribution, whereas we would like it to sample from the possibly-multimodal conditional distribution. Therefore we quantize continuous features into bins, and train XGBoost multiclass classifiers using the softmax objective. We use kernel density integral discretization [McCarter, 2023], which adaptively interpolates between uniform bin-width discretization and quantile-based discretization. At inference time, we take the bin-probabilities for a feature and perform nucleus (top-p) sampling [Holtzman et al., 2019], followed by uniform sampling for a continuous value from within a bin.
For both generation and imputation, we generate features of each sample in random order. For imputation rather than generation tasks, we begin by filling in each sample with the observed values, and run inference on the remaining unobserved features.
Results
Results were obtained always using the default hyperparameters: 20 bins, nucleus sampling at top-p of 0.9, and duplication factor K = 50. Experiments were performed on a decrepit, GPU-broke iMac (21.5-inch, Late 2015) with 2.8GHz Quad-Core Intel Core i5 processor and 16GB memory, while simultaneously running Google Chrome with > 50 open tabs. Experimental scripts are provided with our code. Note that hyperparameter tuning was not done, because it is no fun at all.
Case studies on two smol datasets
Here we compare our approach to ForestDiffusion (with a variance-preserving stochastic differential equation, and default parameters, including T = 50 and duplication factor K = 100). For imputation, we show ForestDiffusion results with and without RePaint [Lugmayr et al., 2022], again using its suggested parameters. In Figure 1, we show results for the Two Moons synthetic dataset, with 200 training samples. We show synthetically-generated data (200 samples) from both methods, on which ForestDiffusion seems to perform a bit better. We also show imputation results, in which we duplicate the input data, mask out the y-axis values, and then concatenate the original and duplicated-with-missing datasets. On this task, we see that UnmaskingTrees strongly outperforms ForestDiffusion.
In Figure 2, we show results for the Iris dataset, specifically plotting petal length, petal width, and species. We show the results for both methods on tabular generation, on which both methods seems to perform equally well. We also create another version of the Iris dataset, with missingness completely at random. In particular, we randomly select samples with 50% chance to have any missingness, and on these samples, we mask the non-species feature values with 50% chance. On this task, UnmaskingTrees and ForestDiffusion with RePaint seem to perform equally well, outperforming ForestDiffusion without RePaint.
Tabular imputation benchmarking
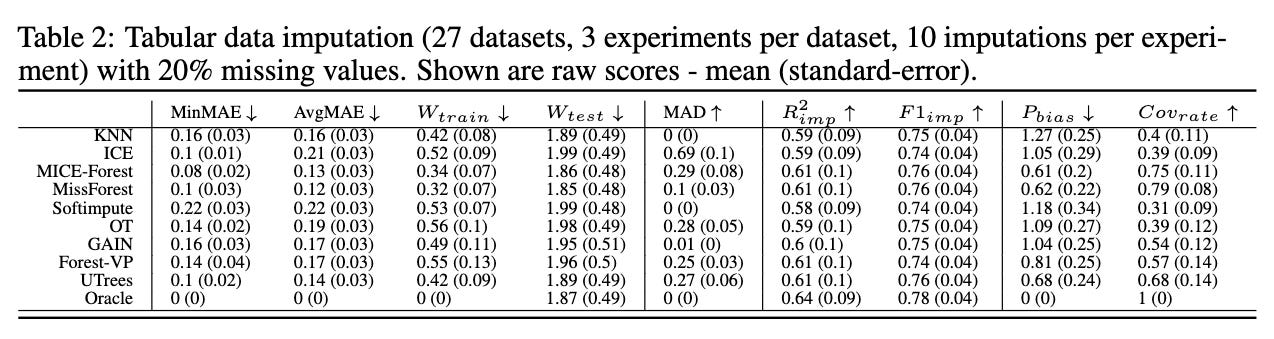
We next repeat the experimental setup of Jolicoeur-Martineau et al. [2024] for evaluating tabular imputation methods. Rank results are shown in Table 1, and raw results are shown in Table 2. UnmaskingTrees does pretty, pretty good.
Discussion
Our proposed approach is basically an instance of autoregressive discrete diffusion framework [Hoogeboom et al., 2021], which has shown great success in a variety of tasks. Furthermore, it can be seen as in line with the common observation, dating back to the development of Vector Quantised-Variational AutoEncoders (VQ-VAEs) [Van Den Oord et al., 2017], that it makes sense to train generative models to predict discrete outputs rather than continuous outputs. Our approach also makes sense in light of the observation that unmasking tends to be superior to denoising as a
self-supervised training task [Balestriero and LeCun, 2024].
Despite their strong outperformance on other modalities, deep learning approaches have laboured against gradient-boosted decision trees on tabular data [Shwartz-Ziv and Armon, 2022, Jolicoeur-Martineau et al., 2024]. Previous work [Breejen et al., 2024] suggests that tabular data requires an inductive prior that favors sharpness rather than smoothness, showing that TabPFN [Hollmann et al., 2022], the leading deep learning tabular classification method, can be further improved with synthetic
data generated from random forests. We anticipate that the XGBoost classifiers may be profitably swapped out for a future variant of TabPFN that learns sharper boundaries and handles missingness.
Finally, we observe where randomness enters into our proposed generation process. Flow-matching injects randomness solely at the beginning of the reverse process via Gaussian sampling, whereas diffusion models which inject randomness both at the beginning and during the reverse process. In contrast, because our method starts with a fully-masked sample, it injects randomness gradually during the generation process. First, we randomly generate the order over features in which we apply the tree models. Second, we do not "greedily decode" the most likely bin, but instead sample according to predicted probabilities, via nucleus sampling. Third, for continuous features, having sampled a particular bin, we sample from within the bin, treating it as a uniform distribution.
Conclusions
Once again, pleez get teh codez, yours free for an unlimited time, at https://github.com/calvinmccarter/unmasking-trees.
References
Randall Balestriero and Yann LeCun. Learning by reconstruction produces uninformative features for perception. arXiv preprint arXiv:2402.11337, 2024.
Felix den Breejen, Sangmin Bae, Stephen Cha, and Se-Young Yun. Why in-context learning transformers are tabular data classifiers. arXiv preprint arXiv:2405.13396, 2024.
Leo Breiman. Random forests. Machine learning, 45:5–32, 2001.
Tianqi Chen and Carlos Guestrin. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, pages 785–794, 2016.
Manbir Gulati and Paul Roysdon. Tabmt: Generating tabular data with masked transformers. Advances in Neural Information Processing Systems, 36, 2024.
Ari Holtzman, Jan Buys, Li Du, Maxwell Forbes, and Yejin Choi. The curious case of neural text degeneration. arXiv preprint arXiv:1904.09751, 2019.
Emiel Hoogeboom, Alexey A Gritsenko, Jasmijn Bastings, Ben Poole, Rianne van den Berg, and Tim Salimans. Autoregressive diffusion models. arXiv preprint arXiv:2110.02037, 2021.
Alexia Jolicoeur-Martineau, Kilian Fatras, and Tal Kachman. Generating and imputing tabular data via diffusion and flow-based gradient-boosted trees. In International Conference on Artificial Intelligence and Statistics, pages 1288–1296. PMLR, 2024.
Andreas Lugmayr, Martin Danelljan, Andres Romero, Fisher Yu, Radu Timofte, and Luc Van Gool. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 11461–11471, June 2022.
Calvin McCarter. The kernel density integral transformation. Transactions on Machine Learning Research, 2023. ISSN 2835-8856.
Ravid Shwartz-Ziv and Amitai Armon. Tabular data: Deep learning is not all you need. Information Fusion, 81:84–90, 2022.
Daniel J Stekhoven and Peter Bühlmann. Missforest—non-parametric missing value imputation for mixed-type data. Bioinformatics, 28(1):112–118, 2012.
Aaron Van Den Oord, Oriol Vinyals, et al. Neural discrete representation learning. Advances in neural information processing systems, 30, 2017.